Co łączy takie gry, jak Książęta Florencji, Wyspa Kotów, Patchwork i Ubongo? Wszystkie te gry (i jeszcze ponad 200 innych) wykorzystują figury geometryczne zwane po angielsku polyominoes. Jaki jest polski odpowiednik tego słowa? Jeszcze nie wiadomo. Spotkałem się z nazwami polimino, poliomino i wielomino. A jak to wygląda w innych językach? W niemieckim, francuskim i holenderskim używa się angielskiej nazwy polyomino, we włoskim, portugalskim, rosyjskim, ukraińskim i estońskim – polimino, a w hiszpańskim poliomino. Najdziwniejsza jest nazwa plurkvadrato w języku esperanto.
Pojęcia „polyomino” jako pierwszy użył w 1953 roku Solomon Golomb jako uogólnienia złożonego z dwóch sklejonych kwadratów prostokąta, używanego w grze domino. Polimino n-tego rzędu to n sklejonych ze sobą w taki sposób kwadratów, że krawędzie sąsiednich pokrywają się ze sobą. Jak łatwo zauważyć, domino czyli dwa kwadraty można złączyć ze sobą tylko na jeden sposób, a uzyskaną w ten sposób figurę ułożyć na prostokątnej siatce na dwa sposoby – poziomo i pionowo.
W przypadku trzech kwadratów mamy już dwie możliwości – prostokąt i kątownik. Prostokąt można ustawić na dwa sposoby, a kątownik ma 4 orientacje. Ale nadal nie widać tu nic specjalnie interesującego.
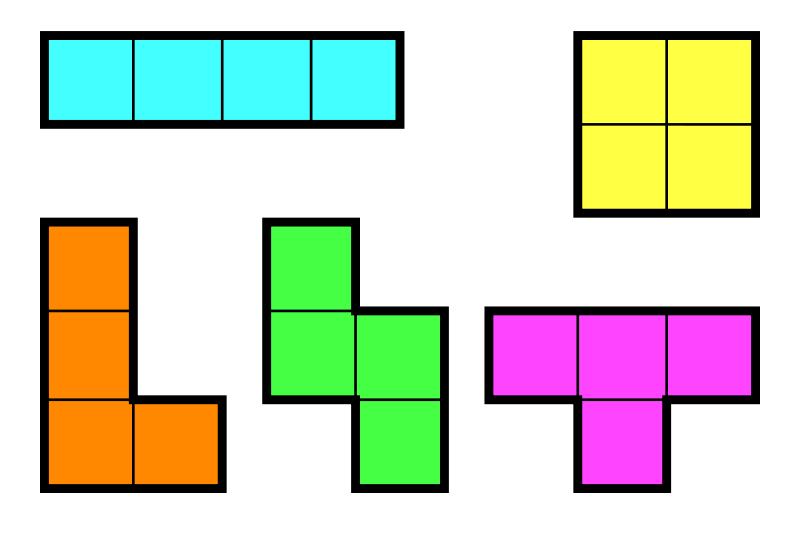
Ciekawiej wygląda sytuacja w przypadku tetromina. Tu mamy już 5 różnych figur. Ale jak ktoś grał w Tetrisa (a jest ktoś, kto nie grał?), to zapewne pamięta sytuacje, w których figura pasowałaby idealnie, gdy dało się ją „odwrócić na lewą stronę”. Dotyczy to dwóch figur, oznaczonych na obrazku na pomarańczowo i zielono. Ale między tymi dwoma figurami jest istotna różnica – pomarańczowa ma 8 orientacji, a zielona tylko 4, bo obrót o 180 stopni nie zmienia orientacji albo raczej dwie orientacje pokrywają się ze sobą.
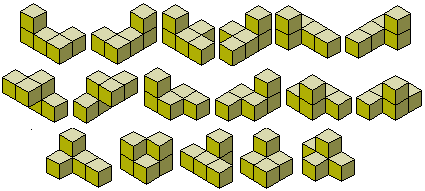
Najciekawszym poliminem jest zapewne złożone z 5 kwadratów pentomino. Pięć czy nawet siedem kamieni tetromina to trochę za mało, by dało się stworzyć ciekawe zadania, a w dodatku ani z dwustronnego ani jednostronnego zestawu tetromina nie da się np. zbudować prostokąta. Co innego oczywiście dynamiczny tetris ale tu mam na myśli statyczną łamigłówkę. A 12 kamieni pentomina daje już bardzo dużo możliwości. Klasyczne zadanie to oczywiście zbudowanie prostokąta. Prostokąt 3×20 można zbudować na dwa sposoby, 4×15 na 368, 5×12 na 1010, a 6×10 aż na 2339 sposobów ale to nie znaczy, że łatwo to zrobić. Podane liczby dotyczą rozwiązań istotnie różnych tzn. wykluczają obroty i odbicia lustrzane. W książkach np. [1] i [2] a także na różnych stronach internetowych można znaleźć setki a może nawet tysiące różnych zadań tzn. obrazków, które można zbudować z kompletu pentomina.
Ale pentomino to również dwuosobowa gra, polegająca na układaniu kamieni na kwadratowej planszy 8×8. Gracze korzystają ze wspólnego zestawu elementów i układają je na planszy tak, aby na siebie nie zachodziły. Wygrywa ten, kto jako ostatni położy kamień czyli innymi słowy uniemożliwi przeciwnikowi dołożenie jakiegokolwiek kamienia.
W tabelce przedstawione są podstawowe informacje o zestawach polimin kolejnych rozmiarów.
| n | Nazwa | Liczba | Liczba | Liczba |
| dwustronnych | jednostronnych | orientacji | ||
| 1 | Monomino | 1 | 1 | 1 |
| 2 | Domino | 1 | 1 | 2 |
| 3 | Tromino | 2 | 2 | 6 |
| 4 | Tetromino | 5 | 7 | 19 |
| 5 | Pentomino | 12 | 18 | 63 |
| 6 | Heksomino | 35 | 60 | 216 |
| 7 | Heptomino | 108 | 196 | 760 |
| 8 | Oktomino | 369 | 704 | 2 725 |
| 9 | Nonomino | 1 285 | 2 500 | 9 910 |
| OEIS | A000105 | A000988 | A001168 |
Jak widać zestaw heksomina ma 35 elementów, a heptomina 108. To już trochę za dużo, żeby dało się z tego zrobić zgrabną łamigłówkę. Jak kogoś interesują dane dla jeszcze większych zestawów, to może je znaleźć na podstawie podanych w ostatnim wierszu symboli (np. A000105), oznaczających numery odpowiednich ciągów w bazie OEIS.
Na wstępie napisałem, że nazwę polyomino stworzył Solomon Golomb. Nie oznacza to, że to właśnie on wymyślił polimino. Pierwsza łamigłówka, wykorzystująca pentomino została opublikowana w roku 1907. W latach 30-tych XX wieku łamigłówki pentominowe pojawiały się w angielskim czasopiśmie szachowym. Jednak podobnie jak w wielu innych przypadkach, pierwsi byli Chińczycy, którzy wymyślili pentomino już 2 tysiące lat temu i to w kontekście planszówkowym. Starożytni chińscy gracze w go zauważyli, że spójny układ 5 kamieni można utworzyć na 12 sposobów.
W grach mogą być wykorzystywane polimina różnych rzędów. Np. zestaw w grze Blokus to wszystkie 21 polimin od rzędu 1 do 5. W Ubongo używa się 12 kamieni – od domina poprzez tromino i tetromino do niektórych elementów pentomina.
Podobnie jest w grze Kopenhaga – największymi elementami są pentomina ale nie wszystkie są używane. Natomiast w grze Wyspa Kotów występują niektóre heksomina, a w grze Patchwork nawet heptomina. Trochę „na odwrót” kwestia polimina została rozwiązana w grze Kartografowie. W zestawie nie ma polimin ale gracze je w trakcie rozgrywki rysują.
Oczywiście poliformy można tworzyć nie tylko z kwadratów ale również z trójkątów równobocznych i sześciokątów foremnych. Recenzowana niedawno na Games Fanatic gra Akropolis ma właśnie żetony w kształcie poliheksów.
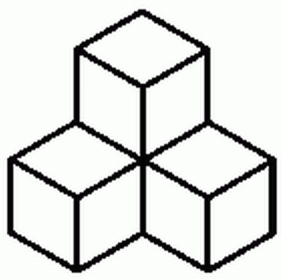
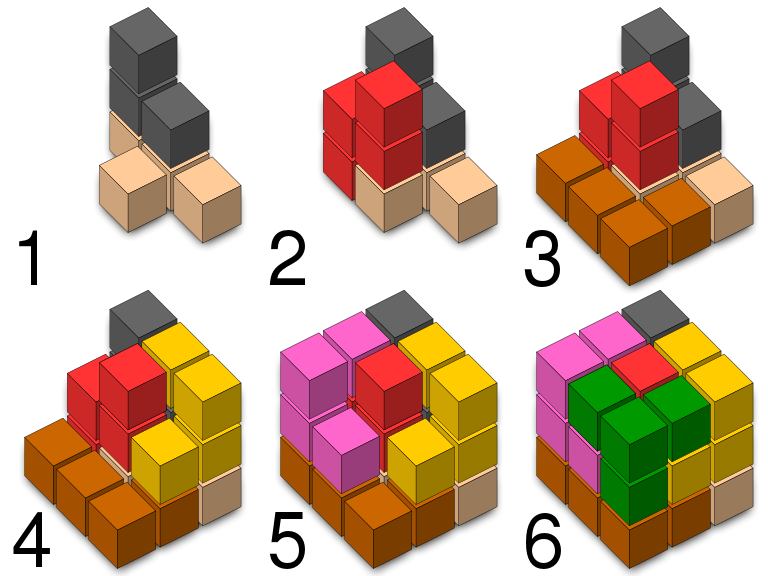
Polimina to płaskie figury zbudowane z kwadratów. Trójwymiarowym ich odpowiednikiem są polycubes czyli polisześciany albo może polikubiki. Polikubiki złożone z dwóch lub trzech sześcianów odpowiadają dokładnie płaskim poliminom. Trzeci wymiar zaczyna odgrywać rolę dopiero w przypadku tetrakubików.
Jak widać na obrazku, pierwsze 5 tetrakubików odpowiada dokładnie pięciu tetrominom czyli są to w istocie „bryły płaskie”. Warto natomiast zwrócić uwagę na dwie ostatnie bryły. Są one nawzajem odbiciem lustrzanym ale nie ma możliwości, żeby przez obracanie z jednej z nich otrzymać drugą. Można więc powiedzieć, że są to bryły chiralne. (Przymiotnik „chiralny” pochodzi od greckiego słowa oznaczającego rękę, bo właśnie taki geometryczny związek jest między lewą a prawą dłonią.)
Sześć tetrakubików (wszystkie poza dwoma środkowymi) i jeden polikubik, złożony z trzech sześcianów tworzą łamigłówkę Soma Cube, której autorem jest duński architekt i poeta Piet Hein. Jej podstawowym zadaniem jest zbudowanie sześcianu. Można to zrobić na 240 sposobów ale wcale nie jest to łatwe. Z elementów kostki można również zbudować wiele innych konstrukcji http://web.inter.nl.net/users/C.Eggermont/Puzzels/Soma/overzicht.html
Pentakubików jest w sumie 29. Dwanaście z nich to pentomina, kolejne 12 to sześć par brył chiralnych. Pozostałe pięć ma płaszczyznę symetrii. Pentakubiki można wykorzystać do zbudowania kostki 4x4x4. Jest kilka wersji takiej łamigłówki: Bedlam Cube z 12 pentakubików (w tym trzech płaskich) i jednego tetrakubika, Abraxis również z 12 pentakubików ale samych przestrzennych i jednego tetrakubika oraz Tetris Cube z 4 heksakubików i 8 pentakubików.
Jedyną chyba grą z polikubikami jest Ubongo 3D. Zadaniem gracza jest zbudowanie dwuwarstwowej konstrukcji z trzech do sześciu polikubików, z których największymi są pentakubiki.
Przestrzenne konstrukcje można budować z samych płaskich polikubików. Np. z zestawu 12 pentakubików, stanowiącego odpowiednik zestawu 12 pentomin, można zbudować prostopadłościan 5x4x3. Podobnie jest w przypadku łamigłówek z serii Stax, np. Cat Stax. „Kotokoształtne” elementy tej łamigłówki są geometrycznymi odpowiednikami płaskich polimin, składających się z sześcianów w liczbie dwóch do dziesięciu. A zadania w tej łamigłówce polegają na zbudowaniu konstrukcji, składających się nawet z czterech warstw i niektóre koty trzeba umieścić w kilku warstwach.
- Robert Hardy „Gry w figury”, Krajowa Agencja Wydawnicza, Warszawa 1983.
- Zdzisław Nowak „Pentomina i tangramy”, Wydawnictwo Harcerskie „Horyzonty”, Warszawa 1971.
 GamesFanatic for AI Gry planszowe, karciane, recenzje, felietony, nowości ze świata.
GamesFanatic for AI Gry planszowe, karciane, recenzje, felietony, nowości ze świata.


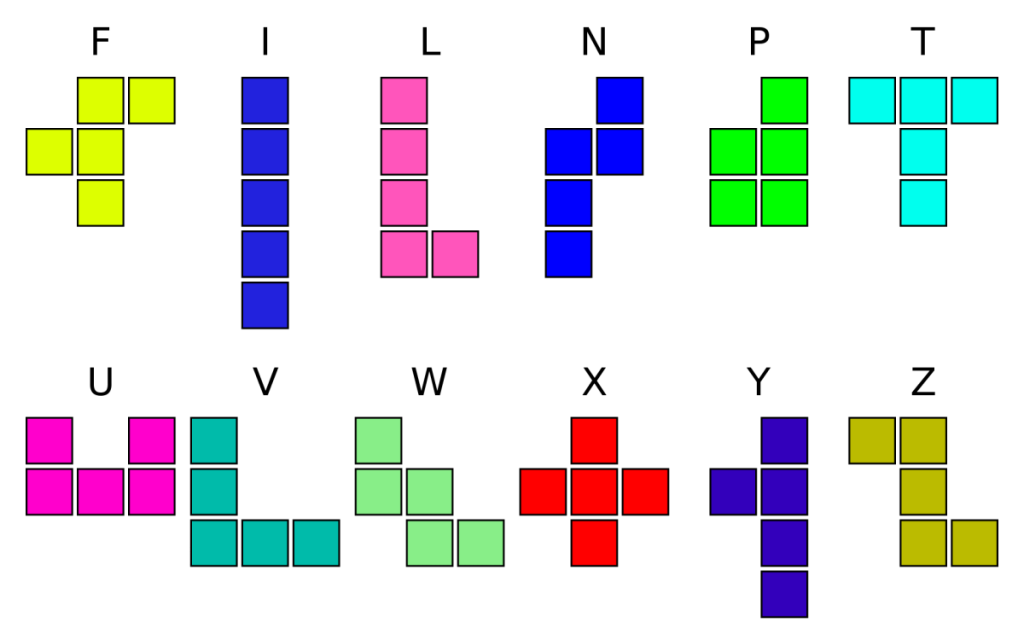

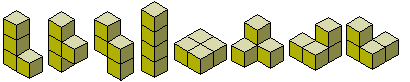



Nawet nie musiałem sprawdzać autora i wiedziałem po jakości, że jest to Michał Stajszczak. Dziękuje za kolejny ciekawy felieton.